Statistical models show that the mean is the best metric to represent the position parameter of a dataset. Many types of moving averages and digital filters have been presented to date to measure this parameter. I propose an original solution to this problem through the Carnazzi filter.
This filter has been designed to combine the qualities of Gaussian and Butterworth filters into a single metric. In traditional filters, the higher the filtering level, the greater the lag. Here we use an innovative technique to get around this problem: instead of increasing the amount of filtering with the cut-off period, we use frequency shifting. This technique provides exceptional responsiveness, while keeping overshoot to a minimum. All of this results to a filter that is as smooth as Butterworth or even Laguerre filter, while retaining the same responsiveness (and even better !) as a Gaussian filter.
In order to measure the performance of this filter compared to a classic Gaussian filter, a Butterworth filter, the Arnaud Legoux moving average (ALMA), or the Hull moving average, I let you consult the benchmarks provided below. The Carnazzi filter also has good computational properties as it calculates extremely fast, especially when compared to the ALMA.
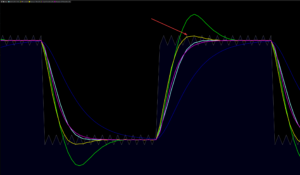
The Carnazzi Filter provides the best representation of a step function :
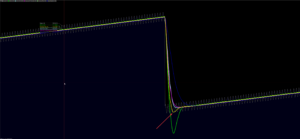
It also nicely handles price gaps :
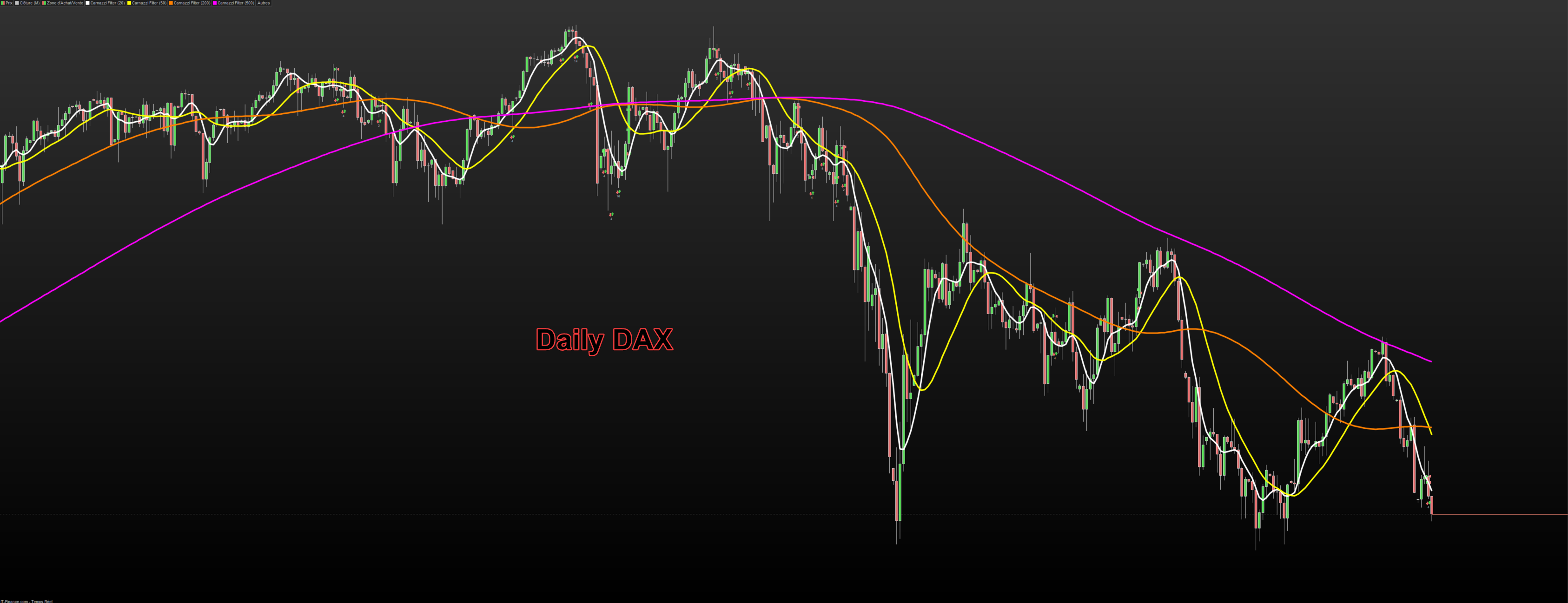
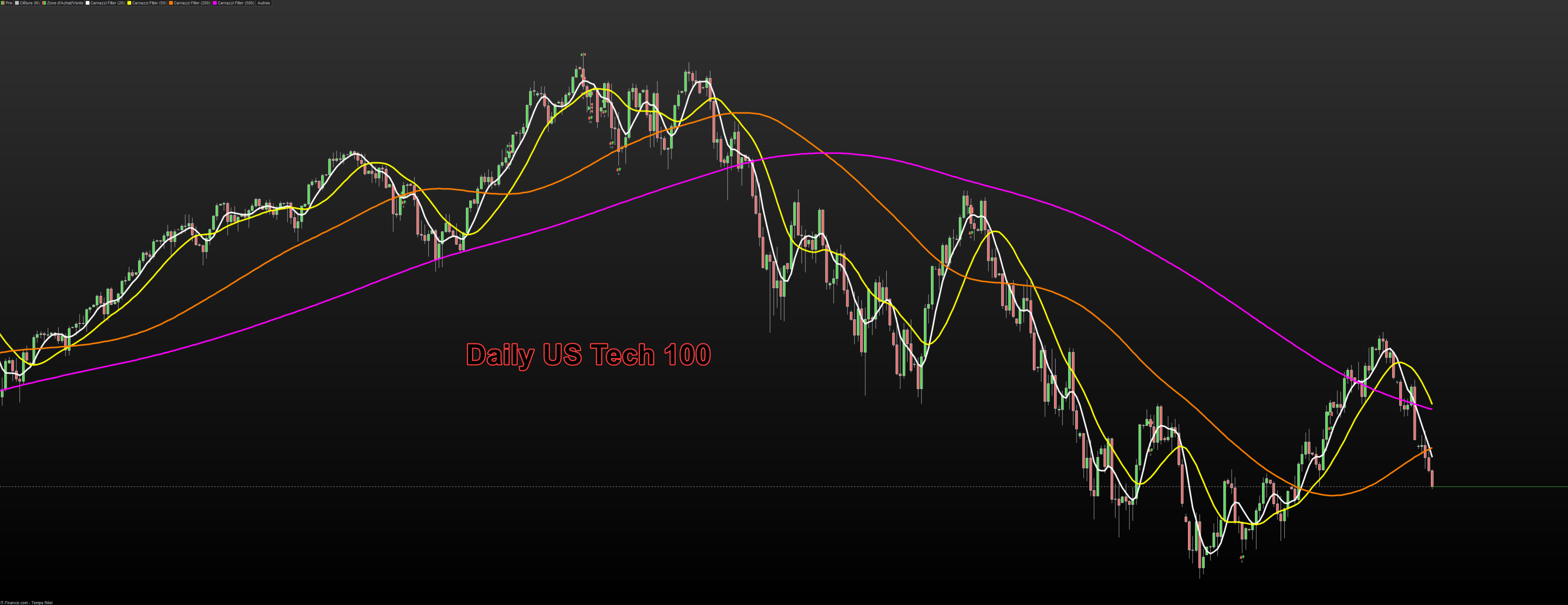
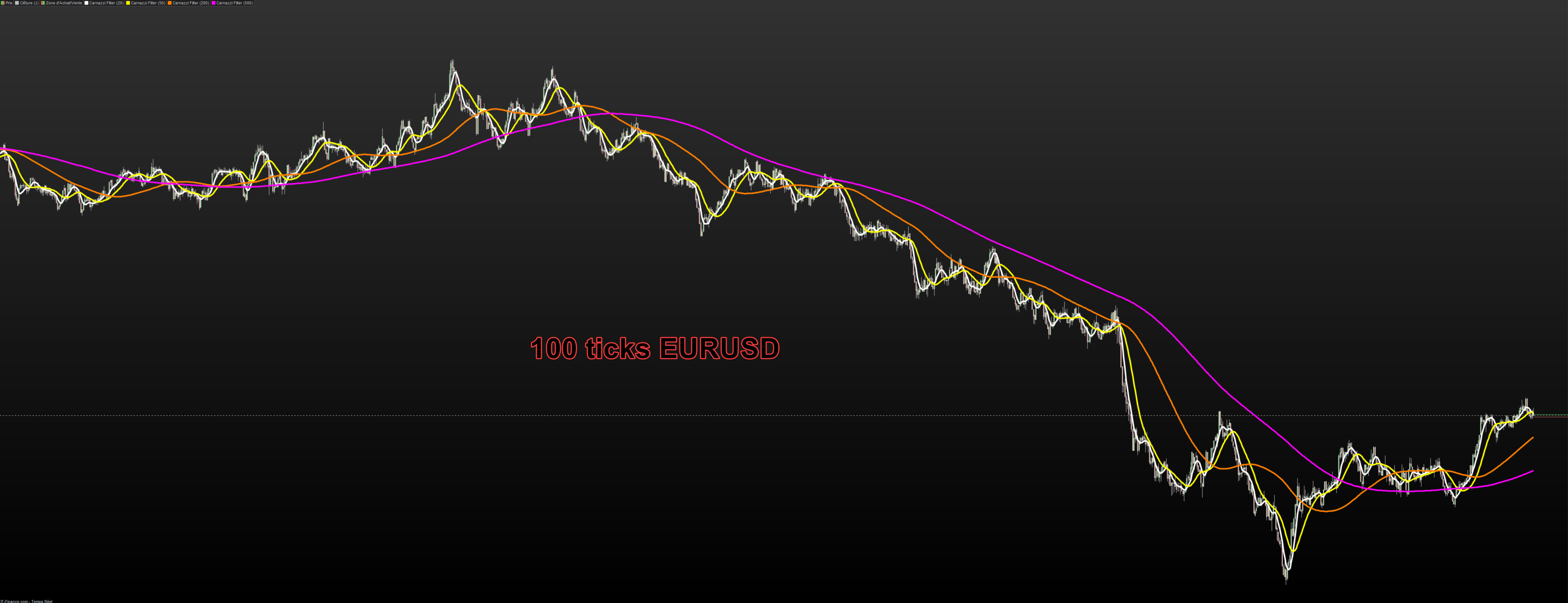
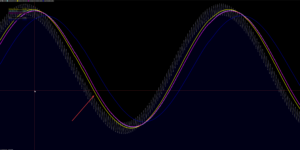
It follows nicely and accurately smooth price movements, even at large period settings :
I am sure that this tool will bring you the greatest satisfaction and I wish you an excellent trading.
Best regards,
Bruno.

t766766 (proprietario verificato) –
this is excellent tool for momentum traders, it give you very early warning when momentum has change, customer service is quick to respond for every inquiry